mnultitool.matrix package¶

Submodules¶

mnultitool.matrix.classification module¶

Functions:

`isMatrixDiagDominant`(A)	Checks if matrix is strictly diagonally dominated
`isMatrixSymmetric`(A)	Checks if a square matrix is symmetric

mnultitool.matrix.classification.isMatrixDiagDominant(A)¶

Checks if matrix is strictly diagonally dominated

Parameters: A (ndarray) – the matrix to be checked
Raises: ValueError – If the supplied np.ndarray does not have exactly 2 dimensions or it is not square
Return type: bool
Returns: whether the matrix is strictly diagonally dominated

mnultitool.matrix.classification.isMatrixSymmetric(A)¶

Checks if a square matrix is symmetric

Parameters: A (ndarray) – the matrix to be checked
Raises: ValueError – If the supplied np.ndarray does not have exactly 2 dimensions or it is not square
Return type: bool
Returns: whether the matrix is symmetric

mnultitool.matrix.matrix module¶

Functions:

`eqSysLUAndSolveJacobi`(A, b, x_init[, …])	Transforms an equation system using LU decomposition and solves the equation system using Jacobi’s method
`eqSysLeastSquaresAndSolve`(A, b)	Transforms an equation system using the least squares method according to the formula:
`eqSysQRAndSolve`(A, b)	Transforms an equation system using QR decomposition and solves the equation system using sp.linalg.solve_triangular
`eqSysRectToSquare`(A, b)	Transforms an equation system with a rectangular matrix of coefficients, to an equation system with a square matrix Note: both the matrix & the vector returned will be different from the inputs
`eqSysSVDAndSolve`(A, b)	Transforms an equation system using SVD decomposition and solves the equation system using sp.linalg.solve
`frobeniusFromPolyCoeffs`(coeffs)	Generates a Frobenius matrix for a given list of polynomial coefficients, ordered from the one next to the highest power of x, to the one next to the lowest (that is, just a scalar)
`svdAndReconstruction`(A, singularValues)	Generates an SVD decomposition of matrix A & reconstructs the matrix using these components and supplied singular values of matrix A

mnultitool.matrix.matrix.eqSysLUAndSolveJacobi(A, b, x_init, epsilon=1e-08, maxiter=100, checkNecessaryCondition=False)¶

Transforms an equation system using LU decomposition and solves the equation system using Jacobi’s method

Parameters

A (ndarray) – a square coefficients matrix A of shape (m, m)
b (ndarray) – vector of right hand side coefficients b of shape (m, 1)
x_init (ndarray) – initial solution of shape (m, 1)
epsilon (float) – the desired solution precision
maxiter (int) – a maximum iterations limit (to prevent an infinite loop), a positive integer

Raises

ValueError – If either input is of invalid type, matrix A does not have exactly 2 dimensions, vector b is of invalid shape, b’s first dimension does not match A’s, matrix A is not square, x_init has an invalid shape, epsilon or maxiter are not positive integers, or matrix A is not strictly diagonally dominant (in such a case Jacobi’s method would not converge)

Return type

ndarray, int]

Returns

a tuple containing (in order): eq sys solution x of shape (m, 1), L, U, iter, where L & U are LU decomposition components and iter is the number of iterations passed

mnultitool.matrix.matrix.eqSysLeastSquaresAndSolve(A, b)¶

Transforms an equation system using the least squares method according to the formula:

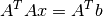
$A^T Ax = A^T b$

and solves the equation system using sp.linalg.solve

Parameters

A (ndarray) – a square coefficients matrix A of shape (m, m)
b (ndarray) – vector of right hand side coefficients b of shape (m, 1)

Return type

ndarray, ndarray, ndarray]

Returns

a tuple containing (in order): vector of eq sys solutions x, transformed matrix A^T A, transformed vector A^T b

mnultitool.matrix.matrix.eqSysQRAndSolve(A, b)¶

Transforms an equation system using QR decomposition and solves the equation system using sp.linalg.solve_triangular

Parameters

A (ndarray) – a square coefficients matrix A of shape (m, m)
b (ndarray) – vector of right hand side coefficients b of shape (m, 1)

Return type

ndarray, ndarray, ndarray]

Returns

a tuple containing (in order): vector of eq sys solutions x, Q, R where Q & R are QR decomposition components

mnultitool.matrix.matrix.eqSysRectToSquare(A, b)¶

Transforms an equation system with a rectangular matrix of coefficients, to an equation system with a square matrix Note: both the matrix & the vector returned will be different from the inputs

Parameters

A (ndarray) – the rectangular coefficients matrix of shape (m, n)
b (ndarray) – vector b of shape (m, 1), containg the right hand side coefficients

Raises

ValueError – When inputs’ types are incorrect or either shape is invalid

Return type

ndarray, ndarray]

Returns

tuple containing a square matrix of shape size (n, n) & a modified vector b of shape (n, 1)

mnultitool.matrix.matrix.eqSysSVDAndSolve(A, b)¶

Transforms an equation system using SVD decomposition and solves the equation system using sp.linalg.solve

Parameters

A (ndarray) – a square coefficients matrix A of shape (m, m)
b (ndarray) – vector of right hand side coefficients b of shape (m, 1)

Return type

ndarray, ndarray, ndarray, ndarray]

Returns

a tuple containing (in order): vector of eq sys solutions x, U, S, V where U, S & V are SVD decomposition components

mnultitool.matrix.matrix.frobeniusFromPolyCoeffs(coeffs)¶

Generates a Frobenius matrix for a given list of polynomial coefficients, ordered from the one next to the highest power of x, to the one next to the lowest (that is, just a scalar)

For example: w(x) = 5x^3 + 4x - 3 => coeffs = [5, 0, 4, -3]

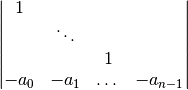
$\setcounter{MaxMatrixCols}{20} \begin{vmatrix} 1 & & & \\ & \ddots & & \\ & & 1 & \\ -a_0 & -a_1 & \dots & -a_{n-1} \end{vmatrix}$

Raises: ValueError – when the input is not a list, or the first coefficient is equal to 0 (and cannot be a divisor then)
Return type: ndarray
Returns: the Frobenius array corresponding to the polynomial with given coefficients

mnultitool.matrix.matrix.svdAndReconstruction(A, singularValues)¶

Generates an SVD decomposition of matrix A & reconstructs the matrix using these components and supplied singular values of matrix A

Parameters

A (ndarray) – matrix A of shape (m, m)
singularValues (ndarray) – singular values vector of shape (m, 1)

Raises

ValueError – When inputs’ types are incorrect or either shape is invalid

Return type

ndarray, ndarray, ndarray, ndarray]

Returns

(U, S, V, M), where U, S & V are SVD decomposition components & M is the reconstruction of A