mnultitool.misc package¶

Submodules¶

mnultitool.misc.approximate module¶

Functions:

`approxZeroBisection`(a, b, f, epsilon, iteration)	Approximates the solution to f(x) = 0 in range [a, b] using bisection method
`approxZeroNewton`(f, df, ddf, a, b, epsilon, …)	Approximates the solution to f(x) = 0 in range [a, b] using Newton’s method
`approxZeroSecant`(a, b, f, epsilon, iteration)	Approximates the solution to f(x) = 0 in range [a, b] using secant method
`coskx1`(k, x)	Computes an approximation of cos(kx) using the formula:
`cossinkx2`(k, x)	Computes an approximation of cos(kx) & sin(kx) using the formulas:
`exponential`(x, n)	Computes an approximation of e^x
`pi`(n)	Computes an approximate value of Pi, using the formula:

mnultitool.misc.approximate.approxZeroBisection(a, b, f, epsilon, iteration)¶

Approximates the solution to f(x) = 0 in range [a, b] using bisection method

Parameters

a (Union`[:py:class:`int, float]) – left range bound
b (Union`[:py:class:`int, float]) – right range bound
f (Callable`[[:py:class:`float], float]) – callable function of variable x
epsilon (float) – the desired precision (stop condition)
iteration (int) – maximum iterations count limit (to prevent an infinite loop)

Raises

ValueError – when input types are wrong or f has same signs on both range bounds

Return type

Tuple`[:py:class:`float, int]

Returns

a tuple containing (in order): an approximate solution x, iterations made count

mnultitool.misc.approximate.approxZeroNewton(f, df, ddf, a, b, epsilon, iteration)¶

Approximates the solution to f(x) = 0 in range [a, b] using Newton’s method

Parameters

f (Callable`[[:py:class:`float], float]) – callable function of variable x
df (Callable`[[:py:class:`float], float]) – callable derivate of f (f’)
ddf (Callable`[[:py:class:`float], float]) – callable second-order derivate of f (f’’)
a (Union`[:py:class:`int, float]) – left range bound
b (Union`[:py:class:`int, float]) – right range bound
epsilon (float) – the desired precision (stop condition)
iteration (int) – maximum iterations count limit (to prevent an infinite loop)

Raises

ValueError – when input types are wrong or either df or dff has same different on both range bounds

Return type

Tuple`[:py:class:`float, int]

Returns

a tuple containing (in order): an approximate solution x, iterations made count

mnultitool.misc.approximate.approxZeroSecant(a, b, f, epsilon, iteration)¶

Approximates the solution to f(x) = 0 in range [a, b] using secant method

Parameters

a (float) – left range bound
b (float) – right range bound
f (Callable`[[:py:class:`float], float]) – callable function of variable x
epsilon (float) – the desired precision (stop condition)
iteration (int) – maximum iterations count limit (to prevent an infinite loop)

Raises

ValueError – when input types are wrong or f has same signs on both range bounds

Return type

Tuple`[:py:class:`float, int]

Returns

a tuple containing (in order): an approximate solution x, iterations made count

mnultitool.misc.approximate.coskx1(k, x)¶

Computes an approximation of cos(kx) using the formula:

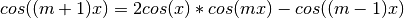
$cos((m+1)x) = 2cos(x) * cos(mx) - cos((m-1)x)$

Parameters

x (Union`[:py:class:`int, float]) – x
k (int) – k

Return type

float

Returns

the approximated value

mnultitool.misc.approximate.cossinkx2(k, x)¶

Computes an approximation of cos(kx) & sin(kx) using the formulas:

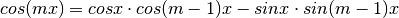
$cos(mx) = cosx \cdot cos(m-1)x - sinx \cdot sin(m-1)x$

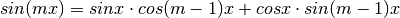
$sin(mx) = sinx \cdot cos(m-1)x + cosx \cdot sin(m-1)x$

Parameters

x (Union`[:py:class:`int, float]) – x
k (int) – k

Return type

Tuple`[:py:class:`float, float]

Returns

approximated cos(kx) and sin(kx) values

mnultitool.misc.approximate.exponential(x, n)¶

Computes an approximation of e^x

Parameters

x (Union`[:py:class:`int, float]) – x
k – k

Return type

float

Returns

the approximated value

mnultitool.misc.approximate.pi(n)¶

Computes an approximate value of Pi, using the formula:

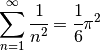
$\sum_{n=1}^{\infty} \cfrac{1}{n^2} = \cfrac{1}{6} \pi^2$

Parameters: n (int) – the amount of sum elements
Return type: float
Returns: the approximated value of pi

mnultitool.misc.norm module¶

Functions:

`maxNorm`(xr, x)	Computes the max norm (sometimes called the ‘infinity norm’) of scalars or vectors; both arguments’ dimensions must be compatible
`residualNorm`(A, x, b)	Computes the matrix norm of the residues of an equation in a form of Ax = b

mnultitool.misc.norm.maxNorm(xr, x)¶

Computes the max norm (sometimes called the ‘infinity norm’) of scalars or vectors; both arguments’ dimensions must be compatible

Parameters

xr (Union`[:py:class:`int, float, List, ndarray]) – precise value, either a scalar or a vector of shape (n, 1)
x (Union`[:py:class:`int, float, List, ndarray]) – approximate value, either a scalar or a vector of shape (n, 1)

Return type

float

Returns

the value of the norm, max(abs(xr - x))

mnultitool.misc.norm.residualNorm(A, x, b)¶

Computes the matrix norm of the residues of an equation in a form of Ax = b

Parameters

A (ndarray) – matrix A (m, m) containing the equation’s coefficients
x (ndarray) – vector x (m, 1) containing the equation’s solutions
b (ndarray) – vector b (m, 1) containing the equation’s right hand side’s coefficients

Return type

float

Returns

matrix norm value of the equation’s residues

mnultitool.misc.rigid module¶

Functions:

`cylinderArea`(r, h)	Computes the total area of a cylinder
`fibonacci`(n)	Computes the first n Fibonacci’s sequence elements

mnultitool.misc.rigid.cylinderArea(r, h)¶

Computes the total area of a cylinder

Parameters

r (float) – cylinder base radius
h (float) – cylinder height

Returns

cylinder area

Return type

float

mnultitool.misc.rigid.fibonacci(n)¶

Computes the first n Fibonacci’s sequence elements

Parameters: :type n: int :param n: the amount of elements

Returns: n first Fibonacci’s sequence elements
Return type: np.ndarray

mnultitool.misc.utils module¶

Functions:

`absoluteError`(v, v_approx)	Calculates an absolute error of two arguments, either scalars, or vectors
`isType`(val, typeArr)	Helper that checks if the supplied value `val` is of a specific type or of a type present in `typeArr`
`relativeError`(v, v_approx)	Calculates a relative error of two arguments, either scalars, or vectors

mnultitool.misc.utils.absoluteError(v, v_approx)¶

Calculates an absolute error of two arguments, either scalars, or vectors

Parameters

v (Union`[:py:class:`int, float, List, ndarray]) – precise value
v_approx (Union`[:py:class:`int, float, List, ndarray]) – approximate value

Return type

Union`[:py:class:`int, float, ndarray]

Returns

absolute error value or NaN if input data is ill-formed

mnultitool.misc.utils.isType(val, typeArr)¶

Helper that checks if the supplied value val is of a specific type or of a type present in typeArr

Return type: bool

mnultitool.misc.utils.relativeError(v, v_approx)¶

Calculates a relative error of two arguments, either scalars, or vectors

Parameters

v (Union`[:py:class:`int, float, List, ndarray]) – precise value
v_approx (Union`[:py:class:`int, float, List, ndarray]) – approximate value

Return type

Union`[:py:class:`int, float, ndarray]

Returns

relative error value or NaN if input data is ill-formed